1. Understanding the Formula
When it comes to understanding formulas, it’s important to grasp the key concepts and principles that underpin them. Whether you’re studying mathematics or diving into the world of science, formulas play a vital role in solving problems and unraveling complex equations.
So, what exactly is a formula? In simple terms, a formula is a mathematical expression that represents a relationship or calculation. It allows us to quantify and analyze various phenomena in a concise and structured manner.
Formulas are the building blocks of quantitative analysis. They enable us to make predictions, perform computations, and gain insights into the behavior of physical and abstract systems.
Now, let’s take a closer look at the components that make up a formula. First and foremost, we have variables. Variables are symbols or letters that represent unknown quantities or values. They serve as placeholders and can take on different values depending on the context.
Next, we have constants. Constants are fixed values that do not change throughout the calculation. They provide the formula with specific numerical values that contribute to the overall calculation.
Variables and constants act as the foundation of the formula. They allow us to introduce flexibility and adaptability into our calculations while maintaining a consistent framework.
In addition to variables and constants, formulas often involve mathematical operators such as addition (+), subtraction (-), multiplication (*), and division (/). These operators dictate the relationship between the various components of the formula and guide the calculation process.
Mathematical operators are the glue that holds the formula together. They determine how the variables and constants interact with each other, ultimately producing a result or solution.
Lastly, formulas can also incorporate functions. Functions are predefined mathematical rules or algorithms that operate on one or more inputs (variables or constants) to generate an output. Functions allow us to perform complex calculations and manipulate data in a systematic manner.
Functions add depth and complexity to formulas. They provide us with specialized tools to analyze specific phenomena or address complex problem-solving scenarios.
By understanding the components and principles of formulas, we can unlock a world of mathematical and scientific possibilities. Whether we’re calculating the trajectory of a projectile, modeling the spread of a disease, or predicting stock market trends, formulas serve as our guiding light in navigating the maze of numbers and variables.
So next time you encounter a formula, don’t be intimidated. Embrace it, dissect it, and unravel its mysteries. Because at the core of every formula lies a treasure trove of knowledge waiting to be discovered.
2. Gathering the Dimensions
Once you have collected all the necessary data for your research, the next step is to gather the dimensions. This involves analyzing the variables and factors that will be used to measure the research objectives.
Identifying the Variables
The first step in gathering the dimensions is to identify the variables that will be studied. These variables can be categorized into two types: independent variables and dependent variables. Independent variables are the factors that are manipulated or controlled by the researcher, while dependent variables are the factors that are measured or observed in response to the independent variables.
For example, if the research objective is to study the impact of advertising on consumer behavior, the independent variable would be the advertisement, while the dependent variables would be the consumer’s purchasing behavior, brand perception, and brand loyalty.
Creating Measurement Tools
Once the variables have been identified, the next step is to create measurement tools. These tools can include surveys, questionnaires, observation forms, or interviews. The measurement tools should be designed in a way that accurately captures the data needed to analyze the dimensions identified in the research objectives.
It is important to ensure that the measurement tools are reliable and valid. Reliability refers to the consistency of the measurement tool in producing similar results when used repeatedly, while validity refers to the accuracy of the measurement tool in measuring what it intends to measure.
To improve the reliability and validity of the measurement tools, a pilot study can be conducted. This involves testing the measurement tools on a small sample of participants to identify any potential issues or areas for improvement.
Collecting the Data
Once the measurement tools have been finalized, the next step is to collect the data. This can be done through various methods, such as online surveys, face-to-face interviews, or collecting data from existing sources.
It is important to ensure that the data collection process is conducted ethically and with integrity. This includes obtaining informed consent from participants, protecting their privacy and confidentiality, and using appropriate data collection methods.
Analyzing the Data
Once the data has been collected, the final step is to analyze the data. This involves organizing, summarizing, and interpreting the data to draw meaningful conclusions and insights.
This can be done using various statistical analysis techniques, such as descriptive statistics, inferential statistics, or regression analysis. The chosen analysis techniques will depend on the research objectives and the type of data collected.
By gathering the dimensions effectively, researchers can ensure that the data collected is accurate, reliable, and valid. This will help in making informed decisions and drawing accurate conclusions from the research findings.
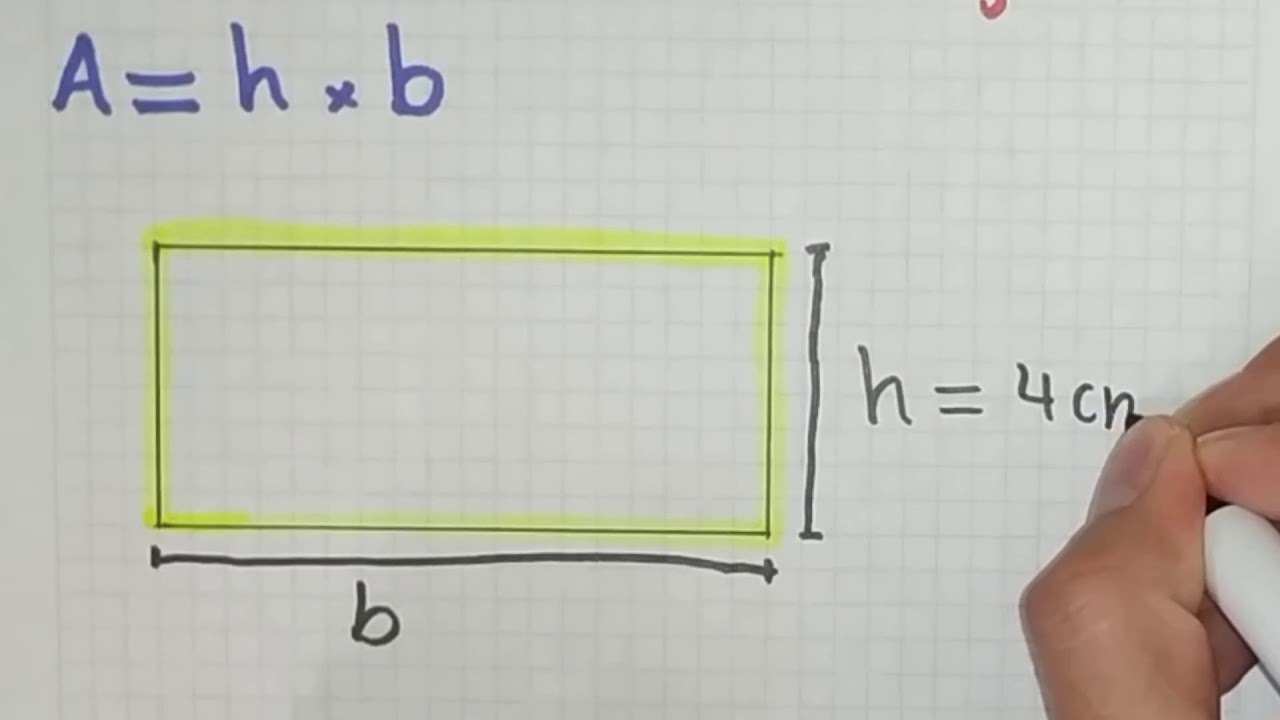
3. Calculating the Area
Calculating the Area
When it comes to finding the area of a shape, there are various formulas that can be used depending on the type of shape. In this blog post, we will explore some common shapes and their corresponding formulas for calculating area.
Square:
A square is a shape with four equal sides. To find the area of a square, all you need to know is the length of one of its sides. The formula for the area of a square is:
Area = side length x side length
Rectangle:
A rectangle is a shape with opposite sides that are equal and four right angles. To find the area of a rectangle, you need to know the length and width of the shape. The formula for the area of a rectangle is:
Area = length x width
Triangle:
A triangle is a shape with three sides and three angles. To find the area of a triangle, you need to know the length of the base and the height of the shape. The formula for the area of a triangle is:
Area = (base length x height) / 2
Circle:
A circle is a shape with a curved boundary and every point on the boundary is equidistant from the center. To find the area of a circle, you need to know the radius of the shape. The formula for the area of a circle is:
Area = π x radius x radius
These are just a few examples of shapes and their corresponding area formulas. Depending on the complexity of the shape, there may be different formulas to use. Remember to always use the correct formula for the specific shape you are working with to calculate the accurate area.
Now that you have a better understanding of how to calculate the area of different shapes, you can apply these formulas in real-life scenarios such as measuring the area of a room or calculating the area of land.
4. Understanding the Result
In order to fully comprehend the outcome of a particular situation or event, it is crucial to analyze and interpret the information at hand. By applying critical thinking and considering various factors, one can gain a deeper understanding of the result.
Key Findings:
- Identify the main objectives or goals that were set and evaluate if they were achieved.
- Take into account any external factors that may have influenced the outcome.
- Analyze the data and statistics to identify trends or patterns.
- Consider any feedback or opinions from stakeholders involved.
By using these strategies, one can effectively interpret the result and make insightful conclusions. It is important to avoid jumping to hasty judgments and instead, take the time to gather all relevant information.
Avoiding Biases: It is crucial to approach the analysis of the result with an open mind and avoid any preconceived biases. This ensures a fair evaluation and allows for a more accurate understanding of the outcome. Being aware of personal biases and actively seeking diverse perspectives can lead to a more comprehensive interpretation.
Conclusion
Understanding the result involves a comprehensive analysis of the available information and a critical approach to interpretation. By avoiding biases and considering various factors, one can gain a deeper understanding of the outcome. This understanding allows for better decision-making and the potential for future improvement.
5. Practice Makes Perfect
Practice is essential when it comes to mastering any skill, and this is especially true for perfecting any craft. Whether you’re learning to play an instrument, honing your artistic abilities, or even working on improving your writing skills, practice is the key to achieving greatness.
With practice, you build muscle memory and develop a deeper understanding of the task at hand. This allows you to perform with confidence and skill, even when faced with difficult challenges. Each time you practice, you are actively reinforcing the neural pathways associated with the skill, making it easier for your brain to access that information in the future.
By setting aside dedicated time for practice, you are prioritizing your growth and improvement. Consistency is key in developing any skill, and regular practice sessions allow you to gradually build upon your previous experiences and achievements.
However, it’s important to note that not all practice is created equal. Simply going through the motions without intention or focused effort may not yield the desired results. It’s crucial to approach each practice session with a specific goal in mind and push yourself to improve a little bit each time.
Remember, practice is not about perfection, but rather about progress. Embrace the process and strive to learn from your mistakes and failures. It’s through these challenges that true growth occurs.
Additionally, it can be helpful to seek feedback from others. Whether it’s a teacher, mentor, or fellow enthusiast, their insights and advice can provide valuable guidance and help you identify areas for improvement.
Lastly, don’t forget to celebrate your achievements along the way. Each milestone reached and goal accomplished is a testament to your dedication and hard work. Take pride in your progress and use it as fuel to continue pushing forward.
In conclusion, practice truly does make perfect. By consistently dedicating time and effort to your craft, you can achieve remarkable results. So, don’t shy away from the challenges that come with practice—embrace them, learn from them, and watch as your skills and abilities soar to new heights.